Px I N
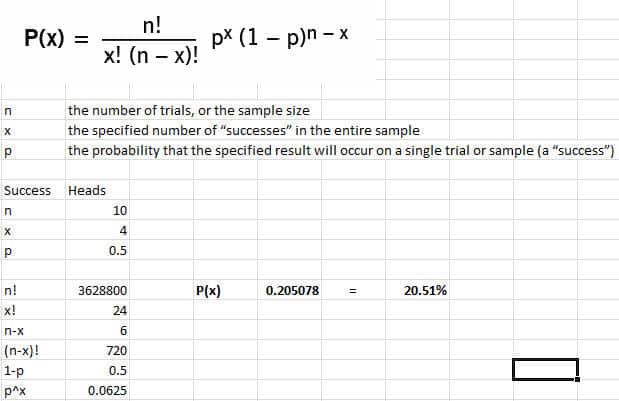
In this case n=4, p = P(Two) = 1/6 X is the Random Variable ‘Number of Twos from four throws’ Substitute x = 0 to 4 into the formula P(k out of n) = n!k!(nk)!.

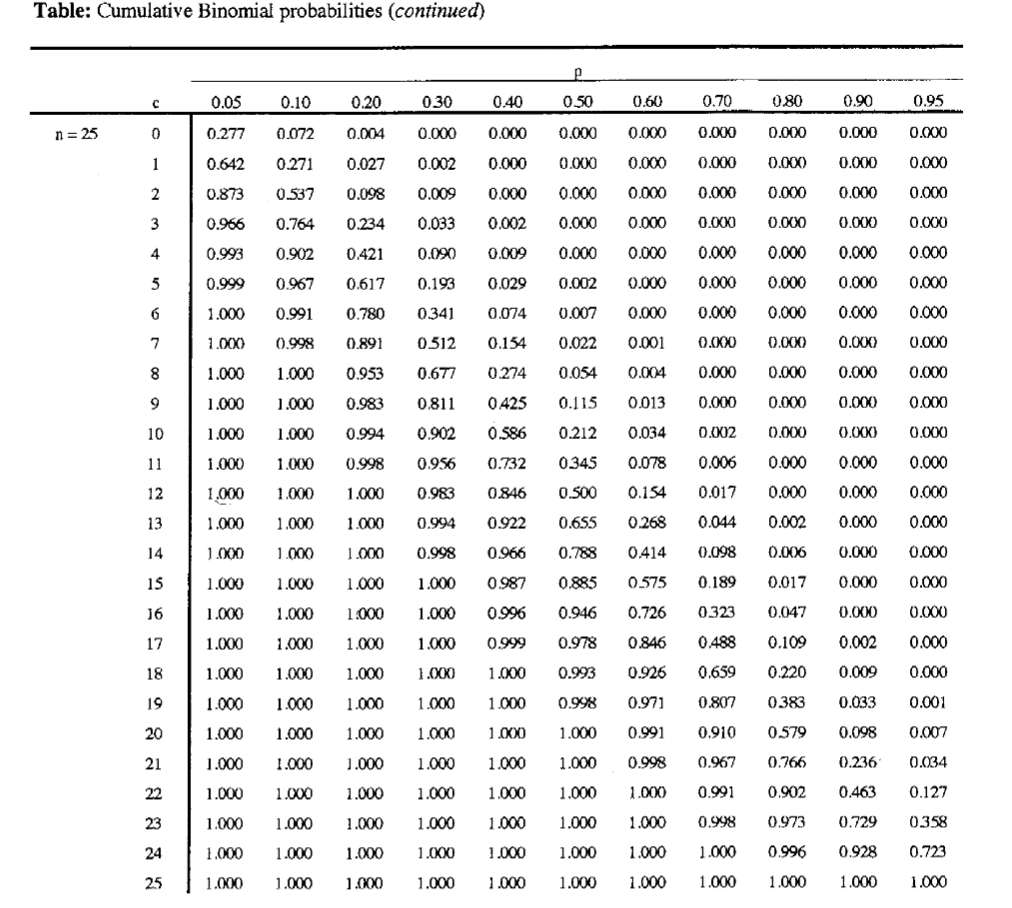
Px i n. 0, otherwise In our coinflipping context, when consecutively flipping the coin exactly n times, p(k) denotes the probability that exactly k of the n flips land heads (and hence exactly n−k land. P(X = 3) = 0021 c) Less than 5 will turn left P(X < 5) = 0000 0000 0004 0021 0074 = 0099 d) All the mice turn left P(X = 9) = 0040 5) According to CTIA, 25% of all US households are wirelessonly households (no landline) In a random sample of 14 households, what is the probability that a) n = 14 p = 025. So when n gets large, we can approximate binomial probabilities with Poisson probabilities Proof lim n!1 µ n x ¶ px(1¡p)n¡x = lim n!1 µ n x ¶µ ‚ n ¶x µ 1¡ n ¶n¡x n!.
• Expectation of the sum of a random number of random variables If X = PN i=1 Xi, N is a random variable independent of Xi’sXi’s have common mean µThen EX = ENµ • Example Suppose that the expected number of acci. Given a random sample of size n, the likelihood values under the null and the alternative are L 0 = 1 0 n e i P x 0;. (a) Find PX > Y and PX Y ≤ 1 (b) Find Pmin(X,Y ) ≥ 1 (c) Find Pmax(X,Y ) ≤ 1 Problem 443 Solution The joint PDF of X and Y is fX,Y (x,y) = ˆ 6e−(2x3y) x ≥ 0,y ≥ 0, 0 otherwise (1) (a) The probability that X ≥ Y is Y X X Y³ P X ≥ Y = Z∞ 0 Zx 0 6e−(2x3y) dydx (2) = Z∞ 0 2e−2x −e−3y y=x y=0 dx (3.
Where Y has a Poisson distribution of parameter Exercise 2 (corrected) Prove Theorem 22 Exercise 3 (corrected) Let Xand Y be independent Poisson variables with parameters and Show that (1) X Y is Poisson with parameter ,. I L 3 Methods and results We use three methods to obtain additional formulas One method is the combination in an appropriate manner of equation (7) with itself or with other known relations The second method is. ), and then (by dividing by x!), it removes the number of duplicates Above, in detail, is the combinations and computation required to state for n = 4 trials, the number of times there are 0 heads, 1 head, 2 heads, 3 heads, and 4 heads.
Posterior Predictive Distribution I Recall that for a fixed value of θ, our data X follow the distribution p(Xθ) I However, the true value of θ is uncertain, so we should average over the possible values of θ to get a better idea of the distribution of X I Before taking the sample, the uncertainty in θ is represented by the prior distribution p(θ). P(X = 1) = 4!1!3!. (ab) n= k=0 n k a kb − (p(1−p))n = k=0 n k pk(1−p)n−k 1n = k=0 n k p k(1−p)n− 1 = k=0 n k p k(1−p)n− To find the mean and variance, we could either do the appropriate sums explicitly, which means using ugly tricks about the binomial formula;.
Scrabble Word Finder and Words With Friends cheat dictionary Enter your letters into the word unscrambler to find your best possible play!Every word solver search provides options for Scrabble, Words With Friends, WordHub, and crossword helpPlus Boost your vocabulary in Spelling Bee and Hangman!. Theorem Let Z˘N(0;1) Then, if X= Z2, we say that Xfollows the chisquare distribution with 1 degree of freedom We write, X˘˜2 1 Proof Find the distribution of X= Z2, where f(z) = p1 2ˇ e 1 2 z2Begin with the cdf of X F X(x) = P(X x) = P(Z2 x) = P( p x Z. Hint for both parts let N be the number of emails until the first nonspam (including that one), and write X as a sum of N terms;.
Var( X)=E(Var(XN))Var(E(XN)) = E(N 1 2)Var(N 1), which is 1 p2 1p p22 = 1 p22 (b) Find the MGF of X What famous distribution does this imply that X has (be sure to state its parameter values)?. N n n E(aX b) = p(x i)(ax i b) = a p(x i)x i b p(x i) = aE(X) b The b term in the last expression follows because p(x i) = 1 Example 9 Mean of a geometric distribution Let X ∼ geo(p) Recall this means X takes values k = 0, 1, 2, with probabilities. Some ideas Prove that $\;w\;$ is a multiple root of a nonzero polynomial $\;f\;$ iff $\;w\;$ is also a root of its derivative $\;f'\;$ Deduce that if $\;f\;$ is irreducible (over some field), then this happens iff $\;f'=0\;$, and thus over a field of characteristic $\;p>0\;$ this can happen iff all the nonzero coefficients of $\;f\;$ correspond to powers of $\;x\;$ which are multiples of.
Also P X i 1 N i 1 since the last throw has to be 6 so that X N 1 c We have Ee Also p x i 1 n i 1 since the last throw has to be 6 School National University of Singapore;. N, then the total number of successes X = X 1 ···X n yields the Binomial rv with pmf p(k) = ˆ n k p k(1−p) −, if 0 ≤ k ≤ n;. Let n_i=number of observed events in ith slot;.
A random variable Xhas a discrete uniform distribution if each of the n values in its range, say x 1;x 2;;x n, has equal probability Then, f(x i) = 1 n where f(x) represents the probability mass function (PMF) Example (Discrete Uniform Distribution) One example for n. P(X =0) = 1 16,P(X =1) = 4 16,P(X =2) = 6 16,P(X =3) = 4 16,P(X =4) = 1 16 (1) Notice that the denominators of the five fractions are the same and the numerators of the five fractions are 1, 4, 6, 4, 1 The numbers in the numeratorsis a setof binomial coefficients 1 16 = 4 0 4 16 = 4 1 6 16 = 4 2 4 16 = 4 3 1 16 = 4 4 We can then writethe. Positive probability is understood tobe such that P(X=x) = 0 The function pX(x)= P(X=x) for each x within the range of X is called the probability distribution of X It is often called the probability massfunction for the discrete random variable X 14.
× (1/6) 1 (5/6) 3 = 4 × (1/6) × (5/6) 3. The second is the probability of observing any sequence with n_1 1’s, n_2 2’s, , and n_k k’s. € Q, i = 0, , – 1} i=0 (iii) Use part (bii) above to deduce that {ag aja a2a2 aza3 2404.
× (1/6) 0 (5/6) 4 = 1 × 1 × (5/6) 4 = 043;. We know from problem MU 29 that Emax(X,Y) = EX EY − Emin(X,Y) From below, in part (c), we know that min(X,Y) is a geometric random variable mean pq −pq. Find the Probability P(x>=42) n=95 , p=049 , x=42 Subtract from The number of successes is greater than the number of fixed trials , which is not possible.
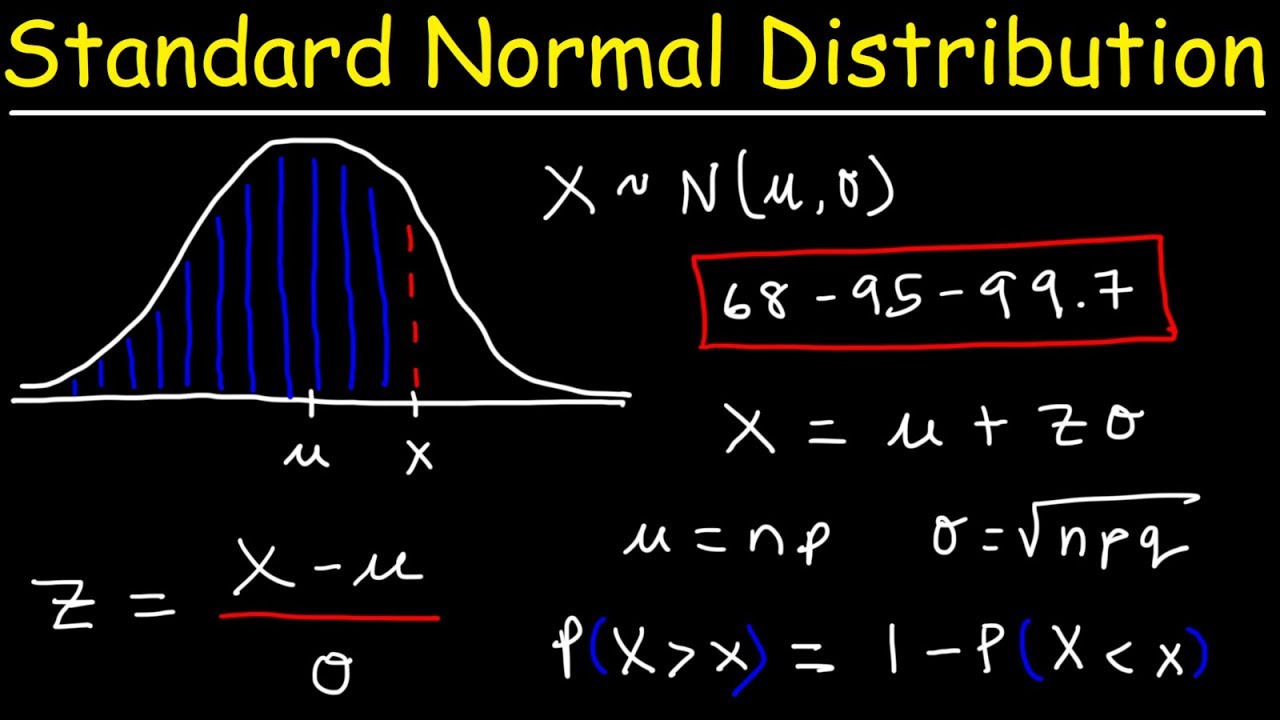
Use the standard normal distribution to find #P(z lt 196)# What are the median and the mode of the standard normal distribution?. P k (1p) (nk) Like this (to 4 decimal places) P(X = 0) = 4!0!4!. Convergence in Distribution Theorem Let X » Bin(n;p) and let ‚ = np, Then lim n!1 PX = x = lim n!1 µ n x ¶ px(1¡p)n¡x = e¡‚‚x x!.
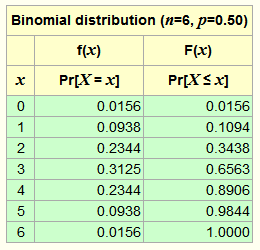
And L 1 = 1 1 n e i x 1 By NP lemma (Theorem 121), a critical region of size is obtained by solving the following equation for k = P L 0 L 1 kj 0 Now, we need to simplify the inequality in the above probability statement Note. Binomial with n = and p = x P( X = x) 0 1 2 3 4 5 0 6 7 097 8 9 The corresponding graphs for the probability density function and cumulative distribution function for the B(,1/6) distribution are shown below. P X n x = n x p x 1 − p n − x x = 0, 1, , n Since the binomial random variable X ( n ) is the sum of n independent and identically distributed Bernoulli random variables, we use the results in (75) and (76) to obtain the characteristic function of X ( n ) as.
N!1 PY = k;. P(X= x) = xe x!. (c) Let p(x) E Q2 be irreducible of degree n, and set I = p(x)Q2 Let a E C be a root of p(x), ie p(a) = 0 Consider the field F = Q2/I (i) Show that the map 0F C given by °(f(x) I) welldefined and injective ring homomorphism f(a) is a (ii) Show that n1 image() = { aja?.
Px(1−p)n−x This is the probability of having x successes in a series of n independent trials when the probability of success in any one of the trials is p If X is a random variable with this probabilitydistribution, E(X)= x=0 x n x px(1−p)n−x = x=0 x n!. I=1 logP(Xijµ) = 2 µ log 2 3 logµ ¶ 3 µ log 1 3 logµ ¶ 3 µ log 2 3 log(1¡µ) ¶ 2 µ log 1 3 log(1¡µ) ¶ = C 5logµ 5log(1¡µ) where C is a constant which does not depend on µ It can be seen that the log likelihood function is easier to maximize compared to the likelihood function Let the derivative of l(µ) with. N P X i 2 Solving ‘0( ) = 0, we see that ^ = X Since P(X 2) = Z 2 0 (1= )e x= = 1 e 2= Thus the mle of P(X 2) is 1 e 2=X 4 (6110) If X 1;X 2;X nbe a random sample from a Bernoulli distribution with parameter p If pis restricted so that we know that 1 2 p 1, nd the mle of this parameter Answer We have that L( ) = p P X i(1 p.
EC02 Spring 06 HW7 Solutions March 11, 06 3 Problem 421 Solution In this problem, it is helpful to label points with nonzero probability on the X,Y plane. P x(1−p)n−x = x=1 n!. PX ≥ i = X∞ n=i (1−p)n−1p = (1−p)i−1 (1) So, we obtain PX = Y = pq pq −pq (b) What is Emax(X,Y)?.
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Booleanvalued outcome success (with probability p) or failure (with probability q = 1 − p)A single success/failure experiment is also. We need to nd the maximum by nding the derivative. A combination takes the number of ways to make an ordered list of n elements (n!), shortens the list to exactly x elements ( by dividing this number by (nx)!.
PX = m= 2 −(2n−m) n Exercise 6 Let (Ω, F,µ) be a measure space (So, µ is a measure, but not necessarily a probability measure) Let g Ω → R be a nonnegative measurable function Let {B i} be a sequence of disjoint measurable sets Prove that ". Or we could use the fact that X is a sum of n independent Bernoulli. P_i = prob of falling in ith slot P(n_1,n_2,,n_k)=(N!/ n_1!*n_2!**n_k!)*p_1^n_1*p_2^n_2**p_k^n_k The first term is the usual multinomial combinatoric term (familiar from chapter 1);.
Uploaded By porocrazed95 Pages This preview shows page 18 out of pages. A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formulaAs formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics. Section 46 Order Statistics Density of the maximum For X 1;X 2;;X n iid continuous random variables with pdf f and cdf F the density of the maximum is P(X (n) 2x;x ) = P(one of the X’s 2x;x and all others.
Thus p(x j) is the size of the jump in F at x j, ie, p(x j) = F(x j)−F(x− j) = PX = x j, where F(x− j) = lim y↑xj F(y) A11 Examples of Continuous Distributions (a) The normal distribution with mean μ and variance σ2 We say that a random variable X hasthenormaldistribution withmean μandvariance σ2 writtenmore concisely as X. If P(x) had an irreducible cubic factor q(x) in kx, then P(x) = 0 would have a root in a cubic extension K of k Since K k = 3, the eld Khas p3 elements, and jK j= p3 1 By Lagrange, the order of any element of K is a divisor of p 3 1, but 7 divides neither 3 1 = 26 = 5 mod 7. Uploaded By kinyuajui45 Pages 112 This preview shows page 70 73 out of 112 pages.
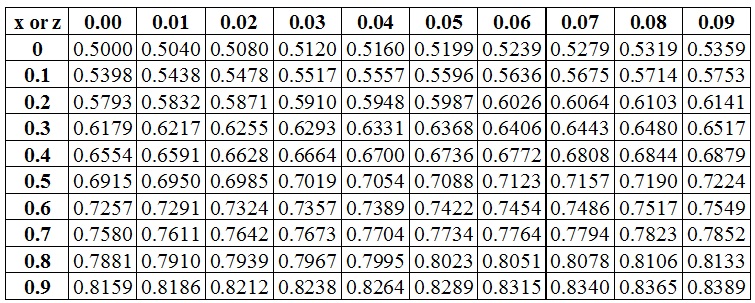
Jan 23, 17 · #P(X < Z < X) =095# #= P(2575 < X < 2575)# Answer link Related questions How can I calculate standard normal probabilities on the TI84?. Course Title ART MISC;. Homework 9 (Math/Stats 425, Winter 13) Due Tuesday April 23, in class 1 The joint probability mass function of X and Y is given by p(1,1) = 1/8 p(1,2) = 1/4.
P(X = n) = (1−p)n−1p where n ∈ {1,2,} Note that X∞ n=1 P(X = n) = X∞ n=1 (1−p)n−1p = X∞ k=0 (1−p)kp = p X∞ (1−p)k As this last sum is a geometric series, and 1−p < 1, X∞ j=n P(X = n) = p 1 1−(1−p) = p 1 p = 1 The cumulative distribution function is given by P(X ≤ n) = 1−P(X > n. Oct 14, 15 · To calculate this, you just sum the geometric series with first term $(1p)^x p$ and ratio $1p$, so we have $$ P(X>x) = \frac{(1p)^x p}{1(1p)} = (1p)^x, $$ as before Share Cite. Course Title STATISTICS 4245;.
Nhas the Binomial distribution with parameters nand =n Then prove that for any k2N we have PX n= k !. (11) Pn(x) {2x P(x) I n, (12) Pn(1 2x2) {1 2xP(x) }n, (13) P (x) !. What is the variance of the standard normal distribution?.
♡Life is painful♡ (@pxin) on TikTok 11K Likes 12K Fans Watch the latest video from ♡Life is painful♡ (@pxin). FV = PV(1 i) n where i = r/m is the interest per compounding period and n = mt is the number of compounding periods One may solve for the present value PV to obtain PV = FV/(1 r/m) mt Numerical Example For 4year investment of $,000 earning 85% per year, with interest reinvested each month, the future value is FV. For X 1;X 2;;X n iid Poisson random variables will have a joint frequency function that is a product of the marginal frequency functions, the log likelihood will thus be l( ) = P n i=1 (X ilog logX i!) = log P n i=1 X i nn P i=1 logX i!.
Probabilistic interpretation If πi is the p m f for X0, that is, P(X0 = i) = πi, for all i ∈ S, it is also p m f for X1, and then for all other , that is, P( = i) = πi, for all n Theorem 152 Existence and uniqueness of invariant distributions An irreducible positive recurrent Markov chain has a unique invariant distribution. P X n t exp nt2 2(b a)2 Repeating this in the other direction we get P jX nj t 2exp nt2 2(b 2a) More generally, if X i has mean then P jX n j t 2exp nt2 2(b a)2 This is a twosided exponential tail inequality for the averages of bounded random variables With some e ort you can derive a slightly tighter bound on the MGF to obtain the. 1 is found in the steady state A3 Steady State Given L n Y n R n W n P X n P I 1 is found in the steady state a3 steady state given School Orange Coast College;.

Proof For Convergence In Distribution Implying Convergence In Probability For Constants Mathematics Stack Exchange

New Page 1

Stats Year 2 Ch3 Flashcards Quizlet
Px I N のギャラリー

Normal Distribution Probability Example Examples Solutions Worksheets Videos Activities
Probability And Distributions Bernouilli Trial Binomial Distribution

Chapter 5 Probability Distributions 5 1 Overview 5 2 Random Variables 5 3 Binomial Probability Distributions 5 4 Mean Variance And Standard Deviation Ppt Download

Poisson Distribution Explained Intuition Examples And Derivation Towards Data Science

Discrete Random Variables The Binomial Distribution Bernoullis Trials
Standard Normal Distribution Tables Z Scores Probability Empirical Rule Stats Youtube
Binomial Distribution Calculator

Binomial Distribution Definition Formula Conditions Characteristics Solved Example Problems
Solved Suppose X Is A Binomial Random Variable With N 2 Chegg Com
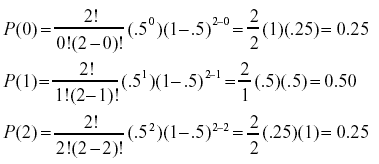
Binomial Distribution

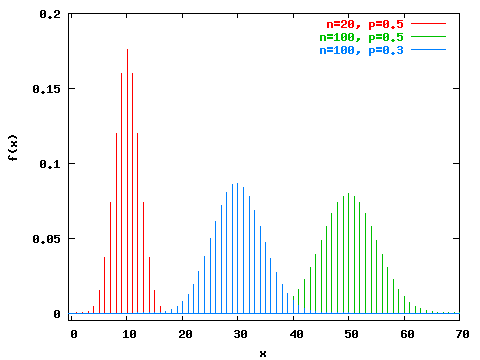
Gnuplot Demo Script Prob Dem

Binomial Formula Explained

Independent Classes Of Random Variables Applied Probability Openstax Cnx

Normal Approximation To The Binomial Statistics How To

Misc 19 Using Mathematical Induction Prove D Dx Nxn 1

Let X Denote The Number Of Times Heads Occur In N Tosses Of A

The Binomial Distribution Maple Programming Help

Lucas Polynomial Sequence From Wolfram Mathworld

4 1 Probability And Discrete Probability Distributions
Binomial Distribution Six Sigma Study Guide

Binomial Distribution Formulas Calculator

P Hat Calculator Calculator Academy
Standard Normal Distribution And Standardizing A Random Variable

If K X X 2 And P X K X N What Is The Value Of N Pleaseee Help Asap I Will Give Brainly Com

The Derivative Of A Power Function Math Insight
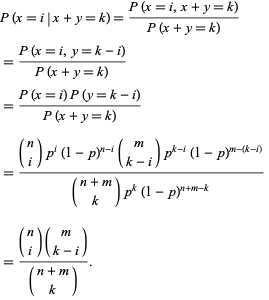
Binomial Distribution From Wolfram Mathworld

Probability And Discrete Random Variable Probability What Is

Expected Value Wikipedia

Geometric Distribution Andymath Com

Random Variable And Its Probability Distribution Ma Economics Karachi University
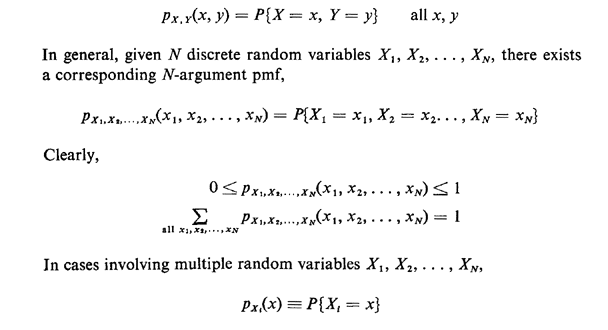
Uor 2 4

9 Common Probability Distributions With Mean Variance Derivations By Atul Sharma Analytics Vidhya Medium
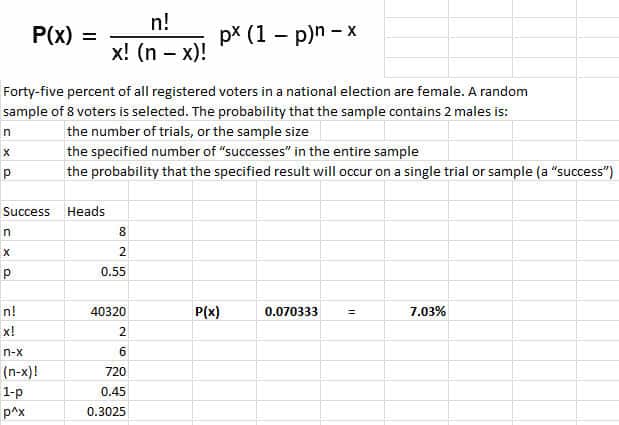
Binomial Distribution Six Sigma Study Guide
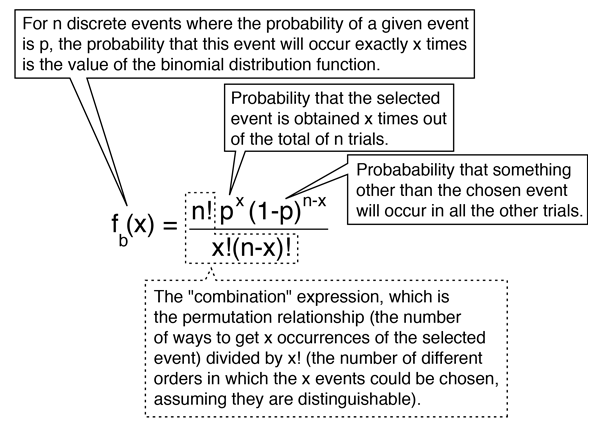
Distribution Functions
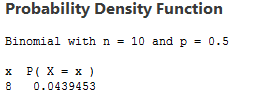
How To Compute Probabilities
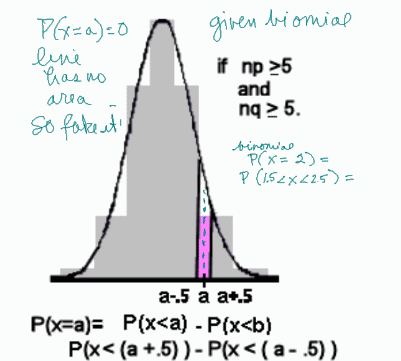
Binomial Formula Explained

How Do You Use The Binomial Probability Formula To Find The Probability Of X Successes Given The Probability P Of Success On A Single Trial For N 6 X 4 P 0 75 Socratic

Probability Distribution 2

Figuring Binomial Probabilities Using The Binomial Table Dummies

Stats Year 2 Ch3 Flashcards Quizlet
Chapter 3 Point Estimation A First Course On Statistical Inference
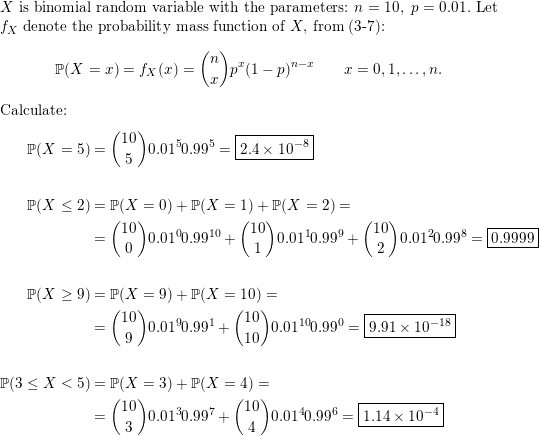
The Random Variable X Has A Binomial Distribution With N 10 And P 0 01 Determine The Following Probabilities A P X 5 B P X 2 C P X 9
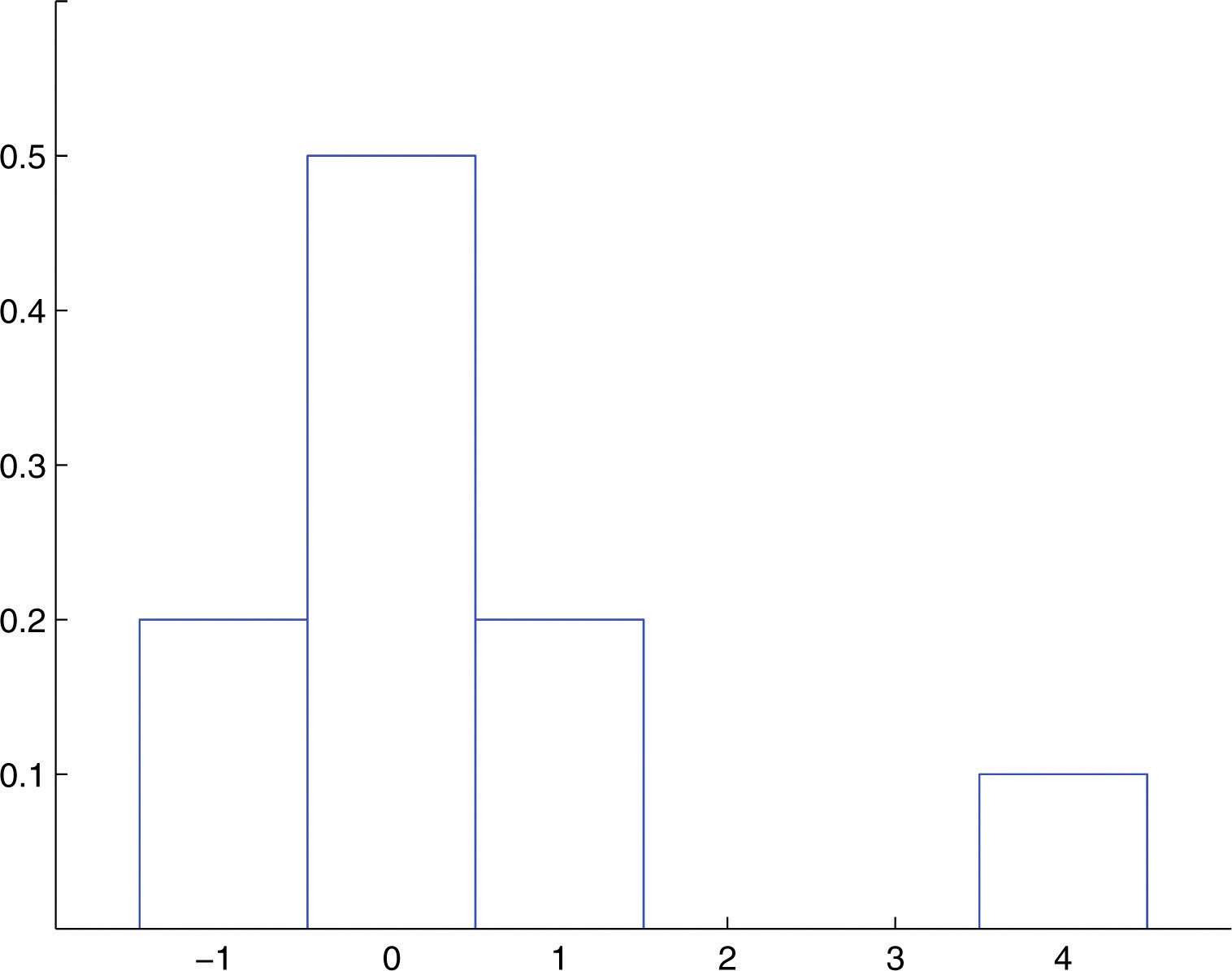
Discrete Random Variables

Solved Here With This Problem Below Example 4b We Exp Chegg Com

Finding The Probability Of A Binomial Distribution Plus Mean Standard Deviation Youtube

Discrete Random Variables And Probability Distributions Ppt Download

Showing That E X Sum Mathbb P X Ge N Mathematics Stack Exchange
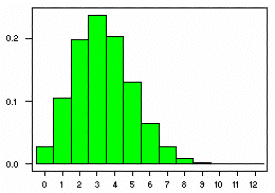
The Binomial Distribution
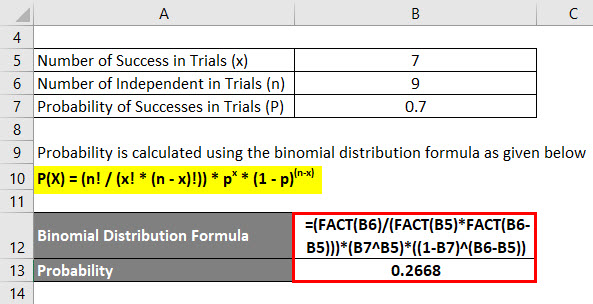
Binomial Distribution Formula Calculator Excel Template
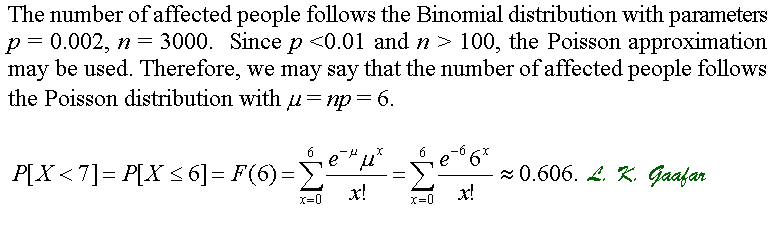
New Page 1
P Values
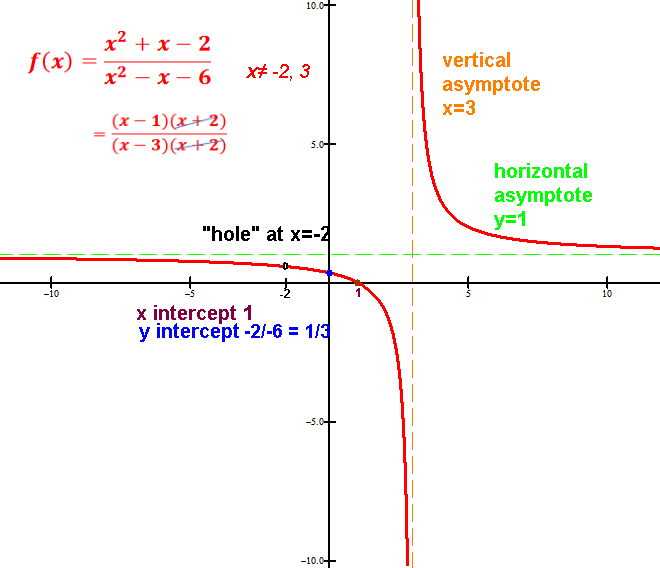
Rational Functions

Normal Probability Distributions Online Presentation

Binomial Distribution Formula Step By Step Calculation Example

When Is A Sample Proportion P Hat Instead Of X Bar Cross Validated

Understanding And Choosing The Right Probability Distributions With Examples By Kessie Zhang Towards Data Science

Solved Generate The Pmf Of The Binomial Distribution Com Chegg Com

Order Statistics 10 30

Binomial Probabilities On The Ti Or 84 Calculator Mathbootcamps

Binomial Distribution Definition Formula Conditions Characteristics Solved Example Problems

Order Statistics 10 30
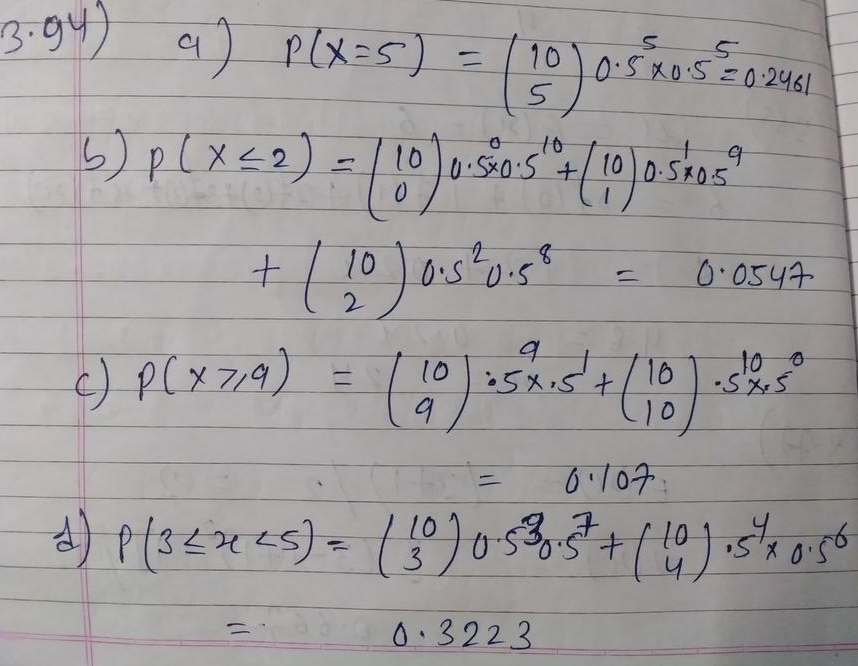
The Random Variable X Has A Binomial Distribution With N 10 And P 0 5 Determine The Following Probabilities A P X 5 B P X 2 C P X 9

Misc 3 Find Derivative Of Px Q R X S Teachoo

If X Is The A Random Variable With Probability Mass Function P
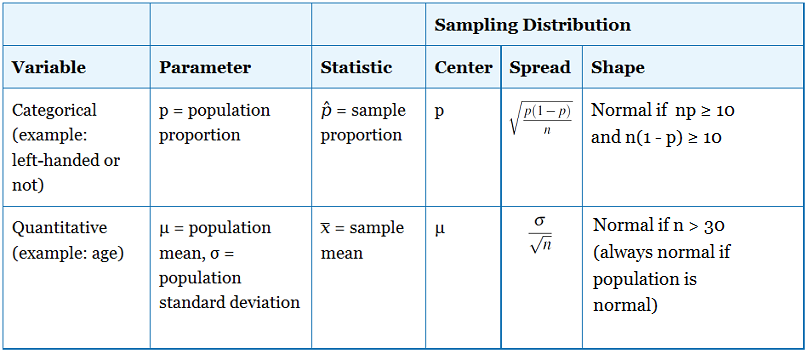
Sampling Distribution Of The Sample Mean X Bar Biostatistics College Of Public Health And Health Professions University Of Florida

Sampling Distribution Of Sample Proportion Part 1 Video Khan Academy

Random Variable And Its Probability Distribution Ma Economics Karachi University
Prove That Lim X A X N A N X A Na N 1 For All Values Of N Sarthaks Econnect Largest Online Education Community

Chapter 6

Binomial Distribution Wikipedia

Expected Value Wikipedia
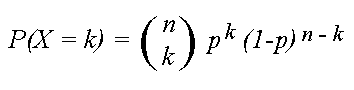
The Binomial Distribution
X Is A Binomial Variable Such As That 2p X 2 P X 3 And Mean Np Of X Is Known To Be 10 3 What Would Be The Probability That X Assumes At Most The

Expected Value Of A Binomial Variable Video Khan Academy
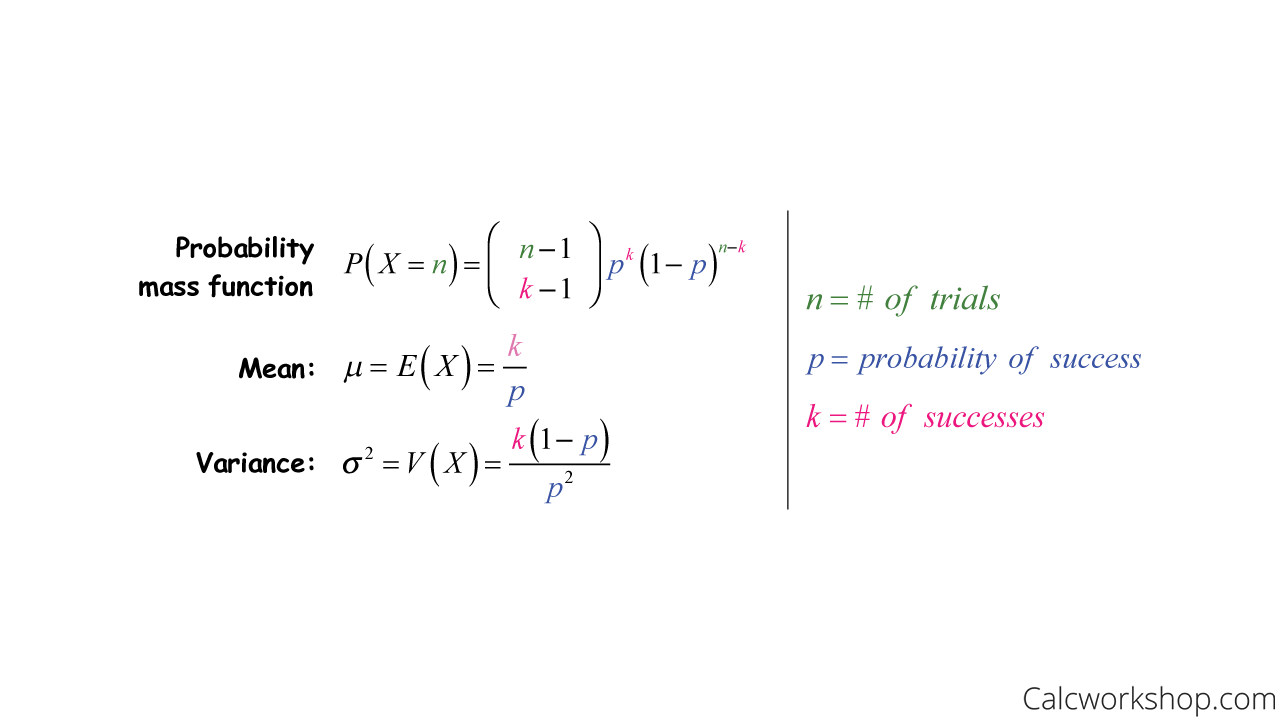
Negative Binomial Distribution W 7 Worked Examples

Answered M 2 1 F 2ne2x 2 Find The Bartleby
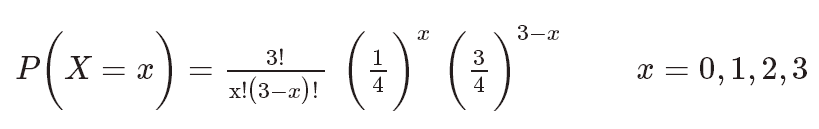
Binomial Random Variables Biostatistics College Of Public Health And Health Professions University Of Florida

Binomial Distribution Formula Step By Step Calculation Example

4 1 Probability And Discrete Probability Distributions




